QUESTIONS ABOUT MODERN CONTROL SYSTEM - ELECTRICAL CONTROL ENGINEERING

 Modern Control System Discreet Data System

1. What is sampling? Write expression for the output of an ideal sampler.

2. What is z-transformation and how it is calculated from Impulse Train Laplace Transformation?

3. Write down some properties of z-transformation.

4. Calculate z-transformation of f(t) = cos ωt.

5. Find z-transformation of f(t) = 1/(s2+2s+2) using sampling time T= 1 second.

6. Determine the z-transform of the finite duration signals

a. 𝑥(𝑛)={0,⃗⃗ 0,1,2,6,−2,3} (Ans= z-2+2z-3+6z-4-2z-5+3z-6)

b. 𝑥(𝑛)={1,2,6,⃗⃗ −2,0,3}

(Hint: Use two sided z-Transform 𝐹(𝑧)=Σ𝑓(𝑘)𝑍−𝑘∞𝑘=−∞

Ans= z2+2z+6+-2z-1+3z-3)

7. Find inverse z-transformation of the function given below given that sampling time T= 1 second by power series and partial fraction method.

𝐹(𝑧)=0.632𝑍𝑍2−1.368𝑍+0.368

8. Solve the difference equation c(k+2)-5c(k+1)+6c(k)=u(k). Given that c(0)=0 and c(1)=1.

9. Solve the difference equation c(k+1)+c(k)=r(k); c(0)=0 by using Z-transform method.

Ans: c(k) = (-2)k-1, k≥1.

10. Derive an expression for Pulse Transfer Function of two cascaded blocks each using a sampler in the input. 

11. Derive an expression for Pulse Transfer Function when only error signal is sampled.

12. Show that the stable region in sampled data control system is inside the unit circle of z-plane. What does outside region of z-plane represent?

13. Explain how Routh-Hurwitz criterion can be applied to sampled data control system?

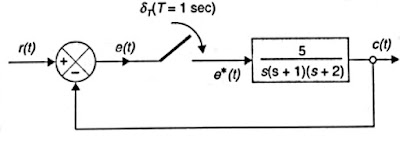
14. Determine the pulse transfer function and stability for the following system using Bilinear transformation.

15. Determine the pulse transfer function and stability for the following system using Bilinear transformation. (Given transfer function of ZOH=(1-e-Ts)/s)

Use comment box below for your answers and more clearification.